|
�@ ���̓x�͏�L���Ђ����w���������܂��Đ��ɂ��肪�Ƃ��������܂����D
����24�N�ŗՏ��H�w�Z�m���Ǝ����o�������\���ꂽ���Ƃɔ������M���ɂ��܂��āC��1�ő�1���Ƒ�1�ő�2���̕ύX�_�����L�Ɏ����܂����D �܂��C���ɂ��܂��Ă������ɒ�������ƂƂ��ɐ[�����l�ѐ\���グ�܂��D 2013�N5��15���X�V |
|||
| �y�[�W | �s�Ȃ� | ��1�ő�1�� | ��1�ő�2���i�����C�ύX�ӏ��j |
| vii�i�ڎ��j | (�^�C�g����萔���āj10 | SI�P�ʌn | �����P�ʌn�iSI�j |
| ix | 30 | �h�v���[���� | �h�v������ |
| �� | 22 | �M�͊w�̑�1�@�� | �M�͊w�̑����@�� |
| �� | ������3 | �Տ��H�w�Z�H�m���Ǝ��� | �Տ��H�w�Z�m���Ǝ��� |
| 4 | 2 | SI�P�ʌn | �����P�ʌn�iSI�j |
| 4 | 7.8 | SI�P���n | SI�P�� |
| 5 | 10 | �i���j�� | �i���j�C |
| 5 | 11 | �Ƃ����� | �Ƃ��� |
| 5 | (�\�g���j5 | �t�F�g�� | �t�F���g |
| 6 | 9 | �����ʂ� | ���s�E1�����j�������ʂ� |
| 6 | 10 | ���߂�� | ���߂�� |
| 7 | 3 | �Ɨ����� | �ŗL�� |
| 7 | 14 | �Ɨ������P�ʖ��ł��� | �ŗL�̖����ł��� |
| 7 | 18 | ������ɂ������ | �������������������� |
| 7 | 19 | �P�ʂł���D���͂̒P�ʁ� | �P�ʂł���C |
| 7 | 21 | �r�h�P���� | �r�h�� |
| 7 | 36 | �P���n | �P�� |
| 7 | 38 | kg/cm2 | kg��/cm2 |
| 8 | 1 | �Ɨ������P�ʖ� | �ŗL���P�ʖ� |
| 9 | 14 | ��p�E����p | ��p����p |
| 11 | 18 | �K�v������ | �K�v�ȗ� |
| 11 | 20 | A�� | A���� |
| 11 | 20 | ������ | ������ |
| 12 | 17 | �}5�� | �}1-3�� |
| 16 | �i�}���j | �V�K�}���jF�����ʂ��EN | |
| 16 | 9 | F�� | F�� |
| 19 | �i�}���j | �a | �b |
| 19 | �i�}���j | �b | �a |
| 19 | �i�}���j | �ԐF���i���j�̈ʒu���ɂ��� | �@ |
| 19 | 11 | �e2�i2�̏��́j | F2 |
| 20 | 25 | �d���� | �d�� |
| 24 | 2 | �\����� | ���\����� |
| 24 | 9 | 12�j���i1-13�j�� | 12�j�����i1-13�j���� |
| 27 | 13 | �P���ł� | �ł� |
| 29 | 8 | �s= | a= |
| 31 | �i�}������}�j | ���E�� | ���Ea |
| 33 | �i�}���j | �K�p�ȗ� | �K�v�ȗ� |
| 35 | �i�}���j |  |
 |
| 37 | 10 | 2���̔��� | 2�K�̔��� |
| 37 | 13 |  |
 |
| 37 | 14 | 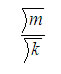 |
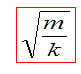 |
| 38 | �iTips���j8 | �ƕ\�����Ă݂�D | �ƕ\���Ă݂�D |
| 38 | �iTips���j12 | ��2���^����2 | ����2�����j��2���^����2 |
| 38 | �iTips���j15 | �i1-38�j�̂悤�� | �i1-38�j���̂悤�� |
| 47 | 18 | ���Ǖǂ̔��ɂ�� | ���Ǖ��������Ȃ邱���ɂ�� |
| 50 | 19-20 | �����D�i���s�j���p��́C | �����D���p��́C |
| 53 | 27 | �̐ϒe������450MPa | �̐ϒe������2.2GPa |
| 59 | 3 | �ƕ\�������D | �ƕ\�����D |
| 59 | �i�\���j | �m��-1�n | �m��-1�n |
| 66 | 5 | �mpa�n | �mPa�n |
| 73 | 13 | ���m�̑��̉t���̍��� | ���m�̑��̉t���̍��� |
| 73 | 13 | ���葤�̉t���� | ���葤�̉t���� |
| 74 | 1 | �mm/s2�n | �mm/s2�n |
| 74 | 5 | ���x1�����[�g���ɂ���� | ���x800�����ȏ��ɂ���� |
| 100 | 6 | /s����60000L/min | /s��60000L/min |
| 109 | 9 | 4.1 | 4-1 |
| 110 | 1 | ������i���s�j���Ԃɂ���� | ����Ɏ��Ԃɂ���� |
| 110 | 3 | �g���`���������̔g������ | �g������ |
| 110 | 4 | ���܁C | 1�����j���܁C |
| 110 | 12 | 4.3 | 4-3 |
| 111 | �i�}���j | X | �� |
| 111 | �i�}���j | 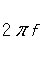 |
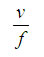 |
| 111 | �i�}���j | ���Ԃ� | �ʒu�� |
| 111 | 5-6 | ���ł���C | �ł���C |
| 111 | 14 | �i4-8�j�� | �i4-8�j���� |
| 112 | Tips���j5 | ���g�������i�e���x�� | ���g�������i�p���x�� |
| 113 | 13 | ��1�i��1��-���j | ��1�i��1��-���j |
| 113 | 14 | ��2�i��2��-���j | ��2�i��2��-���j |
| 114 | 5 | ����ѐU���������ꂼ��a,f�Ƃ� | ������g����a,���Ƃ� |
| 114 | 7 | ���i����-���j | ���i����-���j |
| 114 | 8 | ���i-����-���j | ���i-��2��-���j |
| 114 | 10 | �i���E���j�Ecos(f�E���E���j | �i�����j�Ecos(�����j |
| 114 | 11 | ���_�ŐU���� | ���_�����U���� |
| 114 | 11�` | �i���E���j�C�U������-�i�܂��͔g�������`�ɂȂ�I���̂悤�� | �i�����j�ƂȂ��C-cos(�ւ��j�ɂ������������ԕω��������D���̂悤�� |
| 114 | �i�\���j | �U���F2a�Esin(f�Ex) | �U���F2a�Esin(kx) |
| 115 | 4 | �Ƃ����D�܂��C�U�����ő�ƂȂ镔���Ƃ����D���܂��D | �Ƃ����D�U�����ő�ƂȂ镔���Ƃ����D�܂��D |
| 115 | 4 | sin(f�Ex) | sin(kx)�Ecos�E�i�ւ��j |
| 115 | 6 | ���g�̎����͌��̔g�� | ���g�̎����Ɣg���͌��̔g�� |
| 115 | 7 | �����ɂȂ�D | �����ɂȂ�D�܂��C�U���͌��̔g��2�{�ɂȂ� |
| 115 | 22 | �悢�D�̂� | �悢�D���̂� |
| 115 | 23 | ���j�l����D | ���j���l����D |
| 117 | 2 | �g�̐U����a | �g�̐U����a |
| 117 | 3 | ���g�������Ƃ���C | �g�������Ƃ���C |
| 117 | 4 | f | �� |
| 117 | 6 | �ł���D | ���ʒu���Œ肵����Ԃł̔g�̎��ԓI�ȓ����^����\�����ƂɂȂ�D |
| 117 | 8 | �����g�̑��x���p���x�ւ� | �����g�����ԓI�ȐU��������p���x�ւ� |
| 117 | 10 | ���g�̑��x�ɑΉ�����D | ���ʒu���Œ肵����Ԃł̔g�̎��ԓI�ȓ����^����\�����ƂɂȂ�D |
| 117 | ������3�i�����̂������j�`�Ō� | ������D���ꂪ�_��`���c�g�̑��x�ƂȂ�̂ŁC�g�̑��x���́C�`�ŕ\�킷���Ƃ��ł���D | ������D�U���Ɣg���͗ގ����������������Ă��āC�g���ɂ����Ă͔}���̉^���ɑ��銵���́i�c�|�m����/m3�n�ɑ����j�ƒe���͂ɂ�镜���̗́i�d�ma�n)�ɊW���C�����̗͂̔䂪�g�̓`�����x�ƑΉ�����D |
| 118 | 4 | �i4-26�j | �i4-25�j |
| 118 | 6 | �i4-25�j | �i4-24�j |
| 118 | 6 | �i4-26�j | �i4-25�j |
| 118 | 6 | �i4-25�j | �i4-24�j |
| 118 | 12 | �i4-27�j | �i4-26�j |
| 118 | 20 | �i4-28�j | �i4-27�j |
| 118 | 21 | �i4-26�j | �i4-25�j |
| 118 | Tips���j10 | �i4-25�j | �i4-24�j |
| 119 | 3 | �i4-29�j | �i4-28�j |
| 120 | �}4-10�E���}�^�ړ_ | �@ | �_���Ƌ��E�ʂ̐����n�_�Ɂj�o |
| 121 | 17 | �i4-30�j | �i4-29�j |
| 121 | 22 | �z�C�w���X�̒藝 | �z�C�w���X������ |
| 122 | 5 | �\���͋C�̂ɂ�� | �\�����C�C�̂ɂ�� |
| 122 | 5 | �����I���\���� | �����I�\���� |
| 123 | 7 | �}4-2�Ɏ����悤�����F�� | ���F�� |
| 124 | 8 | �i4-31�j | �i4-30�j |
| 124 | 9 | �i4-32�j | �i4-31�j |
| 124 | 11 | �i4-33�j | �i4-32�j |
| 124 | 16 | �i4-34�j | �i4-33�j |
| 124 | 18 | �i4-35�j | �i4-34�j |
| 125 | 2 | �i4-36�j | �i4-35�j |
| 125 | 4 | �����͂o�_�ɂ����� | �������}���̋��E���ɂ����� |
| 125 | 6 | �i4-37�j | �i4-36�j |
| 125 | �@ | �i4-38�j | �i4-37�j |
| 125 | �@ | �i4-36�j�Ɓi4-38�j | �i4-35�j�Ɓi4-37�j |
| 125 | �@ | �i4-39�j | �i4-38�j |
| 125 | �@ | �i4-40�j | �i4-39�j |
| 125 | �@ | �C���s�[�_���X�Ƃ�C | �C���s�[�_���X������C |
| 125 | �@ | �\�������D | �\�����D |
| 125 | �@ | �i4-39�j | �i4-38�j |
| 125 | �@ | �i4-40�j | �i4-39�j |
| 125 | �@ | �i4-41�j | �i4-40�j |
| 125 | �@ | �i4-42�j | �i4-41�j |
| 126 | 8.10.11 | �h�v���\ | �h�v�� |
| 127 | 1 | �h�v���\ | �h�v�� |
| 127 | 3 | �h�b�v���[���� | �h�v������ |
| 127 | 10 | ��͂���D�͂��߂̓_�r0������̎��b�� | ��͂���D�b�� |
| 127 | 10 | �ȒP�ɂ��邽�߁C�ϑ��҂� | �ȒP�ɂ��邽�����C�Î~�����ϑ��҂� |
| 128 | 3 | �i4-43�j | �i4-42�j |
| 128 | 5 | ��0 | ��0 |
| 128 | 7 | �i4-44�j | �i4-43�j |
| 128 | 8 | �i4.4�j | �i4-42�j |
| 128 | 9 | �i4-45�j | �i4-44�j |
| 128 | 16 | �}4-13�̂悤�� | �}4-14�i���̃S�`�Ɂj�̂悤�� |
| 128 | 23 | s/)�߂Â��Ă���̂ŁC | s/)���߂Â��Ă���̂ŁC |
| 128 | 24 | �ړ������b | �ړ������� |
| 128 | 26 | �b�E | ���E |
| 128 | 26 | �i4-46�j | �i4-45�j |
| 129 | 1 | �i4-47�j | �i4-46�j |
| 129 | 3 | �i4-48�j | �i4-47�j |
| 129 | 8 | �i4-49�j | �i4-48�j |
| 129 | 10 | �i4-50�j | �i4-49�j |
| 129 | 13 | �i4-51�j | �i4-50�j |
| 129 | 16 | �h�v���\���� | �h�v������ |
| 130 | 10 | �i4-52�j | �i4-51�j |
| 130 | 11 | �i4-53�j | �i4-52�j |
| 130 | 15 | �i4-54�j | �i4-53�j |
| 130 | 28 | �i4-54�j | �i4-53�j |
| 131 | 4�`5 | ���̑傫���̐U�������́`�ƂȂ�D | ���̑傫���������I�ɕω�����D���̕ω��̎��g���͎��g���̒Ⴂ�gcos�̍���2�{�i�����������j�ł���C���̔g�̎��g���̍��ƂȂ�D |
| 134 | 1 | �i4-55�j | �i4-54�j |
| 134 | 6 | �i4-56�j | �i4-55�j |
| 134 | 7 | �i4.6�j | �i4-54�j |
| 134 | 8 | �i4-57�j | �i4-56�j |
| 136 | 7 | �i4-58�j | �i4-57�j |
| 137 | ������2 | �r�h�P���ł� | �r�h�ł� |
| 140 | 10 | �i���j�� | �i���j�C |
| 140 | 16.18 | �r�h�P���� | �r�h�� |
| 146 | �}5-5���j | �ړ����� | �`������ |
| 146 | 4 | �ړ����� | �`������ |
| 146 | 15 | ���̊Ԃ��Ԃł��M�̈ړ� | ���̊Ԃ̔M�̈ړ� |
| 148 | 4 | �i�����E�j�j | �����E�j |
| 148 | 5 | �P�ʎ��Ԃ������p | �P�ʎ����C�P�ʑ̐��������p |
| 148 | 6 | �i���Em3�j | ���Em3 |
| 148 | 6 | �P�ʏd�ʂ����� | �P�����ʂ����� |
| 148 | 7 | ���̑g�D��ʉ߂��� | ���̑g�D�P�ʎ��ʂ�������ʉ߂��� |
| 148 | 8 | �i���E�����j | ���E���� |
| 148 | 9 | �i�����E�j�j | �����E�j |
| 148 | 10 | �i���E���j���邢���i���E���E���j | ���E�����邢�́@���E���E�� |
| 148 | 12 | ���t�̉��x�� | �g�D�̉��x�� |
| 148 | 14 | �M�ʂ͒P�ʎ��Ԃ����� | �g�D�P�ʑ̐ρC�P�ʎ��Ԃ�����̔M�ʂ��g�Ƃ���ƁC�g�D�P�ʎ��� |
| 148 | 20 | �ƂɂȂ�D�^���M�ʂ� | �ƂɂȂ�D��莞�����̊Ԃ��^���M�ʂ� |
| 148 | 21 | �^���M�ʁ��s�E | �^���M�ʁ� |
| 148 | 22 | �ł���C���t���e�� | �ł���C�g�D�P�ʎ��ʂ���������t�ʂe�� |
| 148 | 22 | �s | �� |
| 148 | 22�`23 | �Ȃ̂ŁC�i���s�j�P�ʎ��� | �Ȃ̂ŁC�P�ʎ��� |
| 148 | 23 | �P�ʎ��Ԃʼn^��� | �P�ʎ����C�g�D�P�ʎ��ʂ�������^��� |
| 148 | 24�`25 | �s���j�i���s�j�ƂȂ�D | �s���j�ƂȂ�D |
| 148 | 27 | �P�ʏd�ʂ�����̔M�ʂ̕ω��́C���x�ω��� | �P�����ʁC�P�ʎ���������̔M�ʂ̕ω��́C���x�̎����ω��� |
| 148 | 28 | 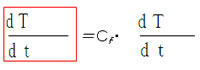 |
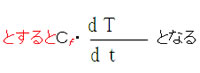 |
| 148 | 34 | P�s�������� | Pt�������� |
| 148 | 35 | P�a | P�� |
| 148 | 39 | �i���Em3�j | ���Em3 |
| 148 | ���}���̓������i9�����j | �� | �� |
| 148 | ���}���̓������i2�����j | ���� | ���� |
| 150 | �}5-6�� | �g�� | ���� |
| 150 | 1 | �����ĉt�� | ���ĉt�� |
| 153 | ������2 | ��<<1�j�̂ŁD | �����s<<1�Ƃ݂Ȃ����j�̂ŁC |
| 158 | ������3 | ���̎��ɏ]���C�`�ł��Ȃ����C0�� | �C�̂̏�ԕ������͗��z�I�ȋC�́i�ȋC�́j�Ő�������D��Âŗp����C�̖̂��x�͔�r�I�����̂ŁC�ߎ��I�ɂ��̕�������K�p����D0�� |
| 158 | ������1 | �̐ς��Ƃ���� | �̐ς��u0�Ƃ���� |
| 159 | 3 | ������ | �������� |
| 161 | ������11 | ��1�@�� | �����@�� |
| 162 | �}5-12�� | ���̂̃l���M�\ | ���̂��G�l���M�[ |
| 163 | 7 | ���݂ł͑�1�@�� | ���݂ł͑����@�� |
| �t�^ | �@ | ����19�N�ŗՏ��H�w�Z�m���Ǝ����o�� | ����24�N�ŗՏ��H�w�Z�m���Ǝ����o���ɍ����ւ� |
-
�J�e�S���ꗗ
���
����
��b��w
�Տ���w
- �Տ���w��ʁE�v���C�}���P�A
- ���ː���w�E�j��w
- ���Ȉ��
- �畆�Ȋw�E�O�Ȋw���
- �f�f�w�E�����f�f�w�E�摜��w
- ���`�O�ȁE�`���O�ȁE�X�|�[�c��w
- �ċz��E�z��E������
- ���@��A�Ȋw�E���O�Ȋw�E��Ȋw
- ���A�a�E������E���
- ��A��Ȋw
- �t��
- �A�t�E�A���E���t�E���ǁE����
- �A�����M�[�E�P���a�E���E�}�`
- �����Ȋw�E�y�C���N���j�b�N
- ���E��ᇈ��
- ��Ð��x�E��ÎЉ�w�E�a�@�Ǘ��E��Ó��v�E��w���
- �����ǁE�G�C�Y
- �\�h��w�E���N�Ǘ��E�n����
- �V�N��w
- �Đ���w�E�Ö@�E���̑�
- �]�_�o�Ȋw�E�_�o�Ȋw
- ��w�̂���݁E��T�y�j���W
- ���_��w�E�S�g��w
- ��w�̂���݁E�ʍ�
- �����ȁE�Y�w�l�Ȋw
- ���A�a�v���N�e�B�X�E�ʍ�
- �����g��w
- �d�q���f�B�A
- �~���|�~�}��w�E�ЊQ��w
�Տ�����
���n�r���e�[�V����
- ���w�Ö@
- �]�����E�����]�@�\��Q
- ��ƗÖ@
- ������Q�E���o�P�A
- ���꒮�o
- ���n�r���e�[�V�����h�{
- �`���E����
- �n�惊�n�r���e�[�V����
- ��U�w�E�����w
- �S�W�E�u���E�V���[�Y
- ��ʗՏ���w
- ���Ǝ�����
- �^���w�E�^���w���K�E�Տ��^���w
- ���T�E���T�E�p��W
- ���n�r���e�[�V������w�E���n�r���e�[�V�����T�_
- CLINICAL REHABILITATION�E�ʍ�
- �V�N���n�r���e�[�V����
- �d�q���f�B�A
- ���퐶�������E�ݑ�P�A
- ������Q
- �^���펾��
- �_�o����
- ���_���n�r���e�[�V����
- �������n�r���e�[�V����
�Ō�
- �Ō�Z�p�E�Ō�ߒ��E�Ō�L�^
- �ꐫ�Ō�
- �Ō�Ǘ��E�N���j�J���p�X
- ���_�Ō�
- �Ō싳��E�Ō쌤��
- �ی��E���Y
- ��p�E�~�}�E�N���e�B�J���P�A
- ����b����/��U�E�a���E���O�q����
- ������E���
- ���Ǝ�����
- �t�E���́E��A��E���B��
- ��앟��
- ���n�r���e�[�V�����Ō�
- �d�q���f�B�A
- ���@��A�E���o�P�A
- ����Ō�E�u�ɊǗ��E�^�[�~�i���P�A
- �����ǁE�����Ǘ�
- �h�{�Ǘ�
- �Տ����l�Ō�
- �ݑ�Ō�E���O�q���Ō�E�n��Ō�E�Ƒ��Ō�
- �V�N�Ō�
- �����Ō�
�h�{
- �h�{�w�E�h�{�Ǘ�
- �����\�E�����\
- �����W
- ���T�E���T
- ��b�h�{�w
- �Ɛ��w�E�����Ȋw���ȏ�
- ���p�h�{�w
- �ۈ�
- �h�{����_�E�h�{�̎w��
- �Տ��h�{�E�Վ�������
- �Տ��h�{�w
- �Տ��h�{�E�ʍ�
- ���O�h�{�w
- �d�q���f�B�A
- ���H�o�c�Ǘ��E���H�̉^�c
- �l�̂̍\���Ƌ@�\�y�ю��a�̐��藧���@��U�E�����E�����w
- �H�ו��ƌ��N�@�H�i�Ɖq���@�H�i�w�E�H�i���H�w
- �H�ו��ƌ��N�@�����w
- �Љ�E���ƌ��N�E���O�q���w
- �Ǘ��h�{�m�{���R�A�J�������e�L�X�g
- �h�{���ȏ����̑�
- ���Ǝ�����
�S��
���Ȉ�t
- ��Ԉ��/����
- �Տ�����
- �N���E���u���b�W
- ���ȗ��H
- �L���`��
- ���o��U/���o�g�D
- �C���v�����g
- ���o�a��/���o������
- �ۑ��C��
- ����
- ��������
- ���Ȗ�
- �����Ö@
- �����w
- ���o�O��
- ������
- ����
- �h�{
- ���ȋ���
- ���w�T�_�E���Ȉ�w����E���Ȉ�w�j
- ��������
- ��ÊǗ�/�X�^�b�t����
- ����X��
- �ی�
- �\�h����/���O�q��
- ���T�E�p��W
- ���ҋ���/�ҍ����}��
- ���ȏ�
- �ېH����
- ���{
- ���o�P�A
- ���ȍ����p�[�t�F�N�g�}�X�^�[
- �Љ�ȁE�㎖�@�E�@��
- �j���[���f�B�A
- ��Q�Ҏ���/�V�N����
- ���E�W�]�ʍ�/��ԗՏ� digital and international�ʍ�
- �אڈ�w
���ȋZ�H�m
- ��������L���O
- �V���E���ꂩ��o��{
- �G��
