やさしさと健康の新世紀を開く 医歯薬出版株式会社

臨床工学講座　医用電気工学 2
（第1版第6刷：2013年1月10日発行）
正誤・補足情報
　
この度は上記書籍をご購入下さいまして誠にありがとうございました．
平成24年版臨床工学技士国家試験出題基準が公表されたことに伴う加筆等につきまして，第1版第5刷と第1版第6刷の変更点を下記に示しました．
また，誤りにつきましてもここに訂正するとともに深くお詫び申し上げます．
2013年5月15日更新
ページ 行など 第1版第5刷 第1版第6刷（訂正，変更箇所）
157 左段7行目 電気を放出して電流を流しますが，出力回路に 電気を放出して電流を流しますが，単相性の除細動器の場合，出力回路に
157 左段9行目 図9-3に除細動器の外観と… 図9-3に単相性の除細動器の外観と…
204 下から4行目 接頭語は累乗よりも計算順序を優先します． 累乗よりも接頭語の計算が優先されます．
231 １４行目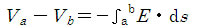
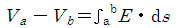付録 　 平成19年版臨床工学技士国家試験出題基準 平成24年版臨床工学技士国家試験出題基準に差し替え

臨床工学講座 医用電気工学 2

（第1版第1刷：2009年4月15日発行）
正誤表

この度は，上記書籍をご購入下さいまして誠にありがとうございました．
以下の箇所に関して誤りがございましたので，ここに訂正するとともに深くお詫び申し上げます．

2010年4月16日更新
頁 行 誤 正
8 演習１最下段 真空中で1m離した単位点電荷どうしに働くクーロン力は9×109Nとなります． 削除
8 演習下の本文１行目 追加 クーロンの法則より，真空中で1m離した単位点電荷どうしに働くクーロン力は9×109Nとなります．
70 ６行目 10mmの間隔で30万Ｖの 10mmの間隔で3万Ｖの
71 問題６の４行目 導体板間距離dを6mm，面電荷密度σを±1pC/m2とする 導体板間距離dを6×10−3m，面電荷密度σを±10nC/m2とする．
71 問題6の図中 [Ｃ ] [ c/m2]
82 演習2　最下段の式 以下のように訂正
【誤】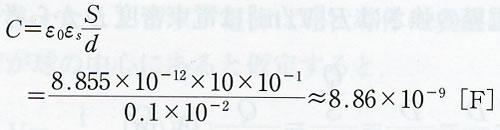


【正】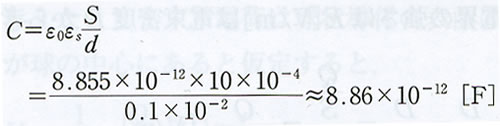
84 2-セラミックコンデンサ・積層セラミックコンデンサの項 以下に差し替え
セラミックコンデンサは，比較的容量が小さい（一般的に0.5pF〜0.1μF）コンデンサで，極性がなく，定格電圧があり高電圧に耐えられます．積層セラミックコンデンサには，極性があるタイプもあり，インダクタンス成分が少なく周波数特性がよいという特徴をもち，小型･大容量化されたチップ型が様々な電子回路基板で用いられています．積層セラミックコンデンサには温度特性の違いにより，誘電体に酸化チタンを用いた低誘電率系と，チタン酸バリウムを用いた高誘電率系の2つのタイプがあります．低誘電率系は誘電率が低いので大容量化には不向きですが，温度による容量変化が小さいというメリットがあります．一方高誘電率系は，誘電率が高いので大容量化できますが，温度による容量変化が−30〜85℃と大きくなるタイプもあります．電解コンデンサと比較した場合の長所としては，異常電圧に対して強いことがあげられます．例えば定格電圧が16Vで静電容量が10μFのタイプで比較した場合，アルミ電解コンデンサの直流破壊電圧が約30Vに対し，積層セラミックコンデンサでは約200Vと高いため，電子機器にパルス電圧やサージ電圧が発生した場合も，絶縁破壊による故障の可能性を低く抑えることができます．
99 演習４　解答（１） コンデンサに蓄えられる電荷は，式（5-22）を用いると コンデンサに蓄えられる電荷は，式（5-21）を用いると
99 演習４　解答（２）最下段 以下のように訂正
【誤】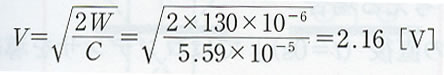


【正】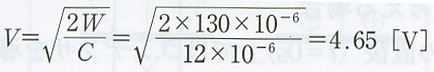
109 演習5中 RC CR
223 第１章・問題２最下段 追加 電荷の符号をどのように仮定しても同じ値となります．
227 第３章・問題3（１） （１）電荷の配置は図のようになっています． （１）電荷の配置を図のように仮定します．
227 第３章・問題3（１）図中 2nC（４つ） 左上から時計回りにそれぞれ，Q1，Q2，Q４，Q３
228 第３章・問題３最後の行 せんね． せん．またこの問題では，すべての電荷から点０までの距離が等しいので，電荷の配置をどのように仮定しても同じ答えとなります．
230 第4章・問題6 以下のように訂正
【誤】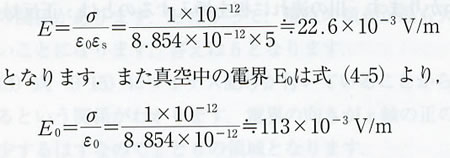


【正】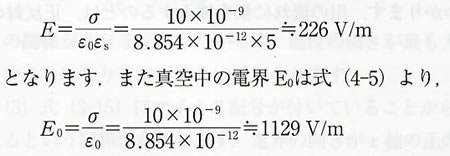
231 第４章・問題6 以下のように訂正
【誤】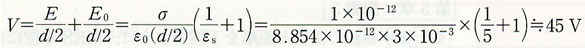


【正】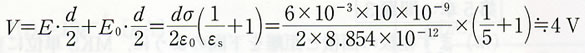
231 第5章・問題1（4） 2×10−6×15＝3×10−3 2×10−6×15＝3×10−5